Java Development
Java – the most common programming language, it is not difficult to learn, so it is suitable for those who first approached the study of programming.
![]()
Java Basic
Introduction Java course is designed for those who are just starting their way in the IT industry and have no idea about the basics of programming.
![]()
Java Pro
During the course, students will learn to create Java applications and gain an understanding of OOP principles. This course is designed for people with basic knowledge in any C-like programming language.
![]()
Java Enterprise
In the process of learning Java Enterprise students will master the EE-technology stack, which is used to create business-level applications and services, which will allow them to become more in demand in the modern IT market.
Our Courses
Java programming course will help you take a comprehensive approach to learning the language and qualitatively master its syntax, capabilities, tools for writing strong projects.

Java Enterprise

Advanced Level

Java Basic
Our Development Companions

This thorough approach positions Avenga as a software testing services and a partner committed to excellence in testing solutions.

Kodjin FHIR Server solutions – your choice to comply with HL7

Innowise, a financial software development company, specializes in creating custom financial solutions, blending innovative design with cutting-edge technology to enhance efficiency and user satisfaction in the finance sector.

Healthcare app development is one of the hottest IT trends of 2023. But a factor that ultimately makes or breaks a business idea is the execution of an app. If you need a professional and experienced dev team, contact Light IT Global right now!

USBoNET (USB over Network) allows users to access remote USB devices via TCP/IP, making them feel locally connected, and facilitating device sharing across diverse locations.

If you’re looking for a reliable and experienced search marketing services provider that can help increase your website traffic, get in touch with Marcin Zygmunt today.

GetDevDone provides pixel-perfect PSD to HTML conversion services. Dedicated project manager, meticulous QA testing, and timely delivery.

Are you looking for developers for your project? EPAM Anywhere Business can help you hire Java developers with niche expertise.

By choosing Syndicode as a reliable Node.js development provider, you will get a secure, stable solution and scalable product for any niche. Collaborate with the best!

Topflight is an award-winning medical app developer. Read this guide about healthcare app development. You will learn more about development steps, mush-have features, budget, and monetization models.
Years Experience
Teachers
Students
Projects
Why Choose our School
We teach only practicing specialists from top IT companies.
The teacher devotes time to each student.
Effective and convenient training.
Urgent issues - timely solution.
Sign Up for Our School
Our Blog
Find out about the latest promotions and discounts, company vacancies, upcoming events and more.

Logitech Wireless Gamepad F710 Review
Continuing our favorite blog topic, we are going to talk about cool gaming accessories. In search of something really interesting, we decided

Innovation Horizons: A Journey Through the Frontiers of Information Technology
Introduction:
Welcome to the vanguard of innovation, where the heartbeat of tomorrow resonates within the sphere of Information Technology

The Impact of AI on Tech Evolution
Artificial Intelligence (AI) is everywhere these days, and it's changing how we live and work. From helping us find the best routes

Demystifying Java Virtual Machine Memory Allocation
When you engage in Java programming, the performance of your application becomes intimately tied to the efficient management of memory, especially when
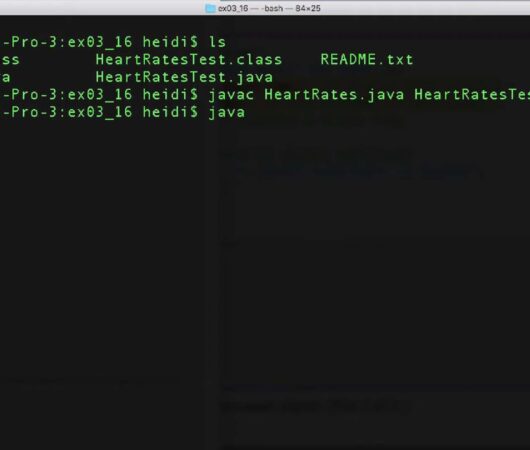
Efficient Handling of Multiple Java Files
Within the dynamic landscape of data administration, the core pillar lies in the realm of storage solutions, which play an indispensable role

JDK Tools: Mastering Troubleshooting Techniques in Java
Java server applications are the backbone of modern web services and enterprise systems, powering everything from online banking to social media platforms.

Java 8 Strings: Efficient String Handling Techniques
In the ever-evolving realm of Java programming, Java 8 has introduced remarkable enhancements, especially in the domain of strings. String manipulation, an

GC Profiler: Unearthing Java Memory Optimization Techniques
In the fast-paced world of software development, every millisecond counts. Whether you're building a high-performance web application or a data-intensive backend system,

Map Reduce Design Patterns Algorithm: Craft Efficient Data
In the ever-evolving landscape of data processing, MapReduce has emerged as a robust paradigm for efficiently handling vast amounts of data. "MapReduce

ArrayDeque vs ArrayList: Analysis and Use Cases in Java
In the world of Java programming, optimizing memory consumption is crucial for building efficient and responsive applications. As developers, we often find

Converting Strings to Any Other Objects in Java
Java is renowned for its flexibility in handling various data types and objects. One of the essential skills every Java programmer should

ArrayList in Java: Unleashing the Power of Dynamic Arrays
In the realm of Java programming, optimizing data structures is essential to ensure that your applications run efficiently. One such versatile data
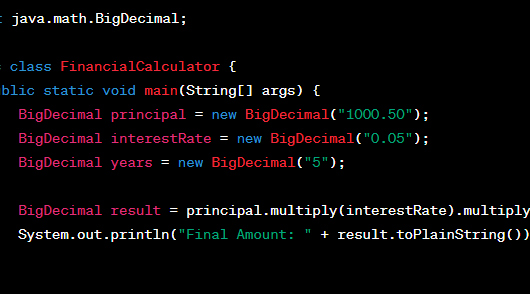
BigDecimal vs. Double in Financial Calculations
In the realm of financial calculations, precision is paramount. The choice between BigDecimal and Double data types can significantly impact the accuracy

Understanding JMH: A Guide to Java Microbenchmarking
Welcome to our in-depth exploration of Java Microbenchmarking Harness, commonly known as JMH. In this comprehensive guide, we will delve deep into
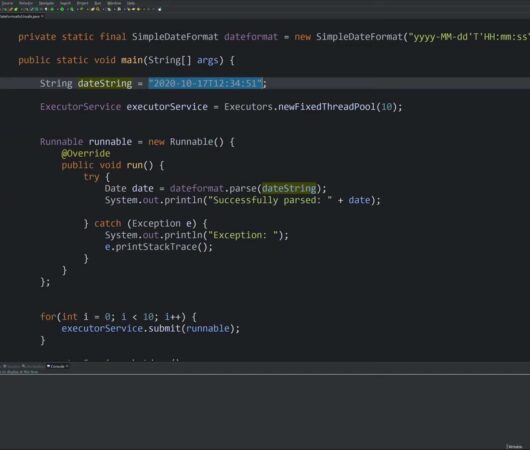
Demystifying Date and Time Handling in Java
The advent of Java 8 marked the introduction of a groundbreaking API, Java Time, more formally recognized as JSR 310. This milestone
Exploring Java's BufferedInputStream Functionality
Java, a multifaceted and object-oriented programming language, empowers developers to deftly maneuver infodata across diverse formats through an array of I/O streams

Enhancing Parsing Efficiency with a FIX Parser
Within the domains of finance and trading, the necessity of a sturdy message processing system cannot be overstated, as it plays a
LinkedList vs. ArrayDeque: A Comparative Analysis
The LinkedList stands as a fundamental pillar in the realm of computer science, playing a significant role in both educational contexts and