In the realm of financial calculations, precision is paramount. The choice between BigDecimal and Double data types can significantly impact the accuracy of your results. In this comprehensive guide, we will delve into the key differences, use cases, advantages, and drawbacks of these two data types. By the end, you’ll have a clear understanding of when to employ each for your financial computations.
Understanding BigDecimal and Double
What is BigDecimal?
BigDecimal is a Java class specifically designed for precise decimal arithmetic. It offers an arbitrary precision decimal type, making it ideal for handling financial calculations that require high accuracy.
What is Double?
Double, on the other hand, is a primitive data type in Java that represents a double-precision 64-bit floating-point number. While it’s suitable for a wide range of applications, it may not always provide the level of accuracy required in financial computations.
When to Use BigDecimal
Decimal Precision Matters
Example: Calculating compound interest, where even a minor rounding error can lead to significant discrepancies over time.
Currency Conversion
Example: Converting between currencies with varying exchange rates necessitates precision to avoid financial losses.
Tax Calculations
Example: Accurate determination of taxes in complex financial transactions.
Risk Assessment
Example: Evaluating investment risks that demand precise calculations to make informed decisions.
Advantages of BigDecimal
- High Precision: BigDecimal allows you to perform calculations with an arbitrary number of decimal places, ensuring accuracy.
- Avoids Rounding Errors: It eliminates rounding errors associated with floating-point arithmetic, making it suitable for financial applications.
- Exact Representation: BigDecimal can represent exact decimal values, which is essential for financial regulations and compliance.
When to Use Double
Performance-Critical Applications
- Example: Real-time simulations and graphical rendering, where speed is more critical than precision.
Scientific Computing
- Example: Complex scientific simulations where absolute precision is less critical than computational speed.
Advantages of Double
- Efficiency: Double offers faster performance compared to BigDecimal due to hardware support for floating-point operations;
- Simplicity: It’s easier to work with Double in simpler scenarios where a high degree of precision is not required.
BigDecimal vs. Double
| Criteria | BigDecimal | Double |
|---|---|---|
| Precision | High precision with arbitrary decimal places | Limited precision with 15-17 significant digits |
| Use Cases | Financial calculations, currency conversion | Performance-critical applications, scientific computing |
| Rounding Errors | Rare, as it eliminates most rounding errors | Common due to floating-point limitations |
| Memory Usage | Higher due to storage of additional information | Lower due to the simplicity of representation |
| Speed | Slower due to complex arithmetic operations | Faster due to hardware support for floating-point operations |
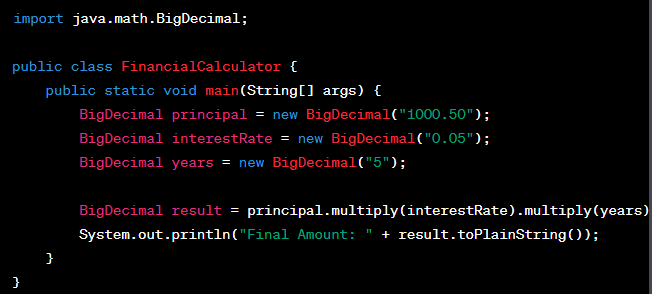
Code Snippet: BigDecimal Usage
Importance of Choosing Wisely
The choice between BigDecimal and Double in financial calculations should not be taken lightly. A single miscalculation can have far-reaching consequences in the financial world. Consider your specific requirements and the level of precision your calculations demand before making your choice.
Common Pitfalls and Best Practices
When working with BigDecimal and Double in financial calculations, it’s essential to be aware of common pitfalls and adopt best practices to ensure accuracy and reliability.
Common Pitfalls
- Inappropriate Precision: Using BigDecimal with excessive decimal places can lead to unnecessary complexity and increased memory usage. Ensure that you choose an appropriate level of precision for your calculations;
- Data Type Conversion: Switching between BigDecimal and Double without careful consideration can result in precision loss, leading to inaccuracies in your calculations. Be mindful of data type conversions.
Best Practices
- Use the Right Data Type: Choose the data type that aligns with the specific needs of your financial application. Opt for BigDecimal when precision is paramount, and use Double when performance is crucial;
- Avoid Comparing Floating-Point Numbers: When working with Double, avoid direct comparisons due to the inherent imprecision of floating-point numbers. Instead, use tolerance-based comparisons;
- Round at the End: If you’re using BigDecimal, perform rounding only at the final step of your calculations to minimize rounding errors.

Real-World Examples
To illustrate the practical implications of choosing between BigDecimal and Double in financial calculations, let’s explore some real-world scenarios.
Scenario 1: Mortgage Calculations
Imagine you’re developing a mortgage calculator for a financial institution. In this case, precision is paramount. Using BigDecimal allows you to handle complex interest calculations with utmost accuracy, ensuring that borrowers receive precise repayment schedules.
Scenario 2: Stock Market Analysis
For real-time stock market analysis, speed is essential. Double is the preferred choice here, as it offers the necessary computational efficiency to process large volumes of data quickly. However, it’s crucial to be aware of the inherent limitations of floating-point arithmetic when dealing with financial data.
Comparative Analysis: BigDecimal and Double in Action
Let’s examine a side-by-side comparison of how BigDecimal and Double perform in a sample financial calculation scenario: calculating the net present value (NPV) of an investment.
NPV Calculation
Suppose you’re calculating the NPV of an investment with the following details:
- Initial investment: $10,000;
- Expected cash flows over five years: $2,000, $2,500, $3,000, $3,500, $4,000;
- Discount rate: 5%.
Using BigDecimal
1. Calculate the NPV using BigDecimal with high precision:
NPV = $2,000 / (1 + 0.05)^1 + $2,500 / (1 + 0.05)^2 + $3,000 / (1 + 0.05)^3 + $3,500 / (1 + 0.05)^4 + $4,000 / (1 + 0.05)^5
2. The calculated NPV using BigDecimal is $11,412.28 (rounded to two decimal places).
Using Double
1. Calculate the NPV using Double:
NPV ≈ $2,000 / (1.05)^1 + $2,500 / (1.05)^2 + $3,000 / (1.05)^3 + $3,500 / (1.05)^4 + $4,000 / (1.05)^5
2. The calculated NPV using Double is approximately $10,612.24 (rounded to two decimal places).

Conclusion
In the world of financial calculations, precision is non-negotiable. BigDecimal shines when accuracy is paramount, ensuring that rounding errors are minimized. On the other hand, Double offers speed and efficiency for scenarios where absolute precision takes a back seat to performance.
Remember, the key to success in financial calculations lies in selecting the right tool for the job. Whether it’s the exactitude of BigDecimal or the speed of Double, your choice should align with the specific demands of your financial application.
FAQs
Use BigDecimal when precision is crucial, such as in compound interest, currency conversion, tax calculations, and risk assessments.
Double offers better performance and is suitable for applications where speed is more critical than precision.
To minimize rounding errors, opt for BigDecimal, as it allows for precise decimal arithmetic.
BigDecimal can be slower and consume more memory compared to Double, which may not be suitable for all applications.
Yes, you can convert between these data types as necessary, but be mindful of potential precision loss when transitioning from BigDecimal to Double.